Tony Foale Designs, article on motorcycle tyre characteristics and how they work.

CAMBER THRUST

© Tony Foale 1985 -- 1997

In the previous article we looked at the basic balance stability needs of the single track vehicle, and the next logical thing to consider would seem to be the only connection that our machines have with mother earth, i.e. the tyre road interface.

LAWS OF NATURE

When Newton first expounded to the world his theories of mechanics, no doubt he had on his mind, things other than the interaction of motorcycle tyres with the road surface. Never-the-less his suppositions are equally valid for this situation. In particular the one that states, "For every force there is an equal and opposite force to resist it." or to put it another way "Action and reaction are equal and opposite." Relating this to tyre action, means that when the tyre is pushing on the road then the road is pushing back equally hard on the tyre. This applies equally well regardless of whether we are looking at supporting the weight of the bike or resisting cornering, braking or driving loads. What this particular law of Newton does not concern itself with, is which force is the originating one nor indeed does it matter for many purposes of analysis. But, as a guide to the understanding of some physical systems it is valuable to know. The forces that occur between the ground and the tyres determine so much the behaviour of our machines, but they are so often taken for granted.

BRAKING

As the brake is applied a torque is transmitted through the wheel to the contact patch, where it manifests itself as a linear horizontal force at the road surface. The road pushes backward on the tyre and with equal intensity the tyre pushes forward on the road. Under power the situation is similar except that the direction of the forces are reversed. This is all fairly obvious and easy to understand, the tyre initiates the action and the road reacts to it.

CORNERING

It is when we wish to study the action of cornering forces and how these are generated that things become a little cloudy. As we negotiate a curve, centrifugal (centripedal for the purists, although these terms only represent the action and reaction to each other) forces are generated as a consequence of the bike's desire to travel on in a straight line. You msy to get otc bv. To counter this desire the road must react with the tyre to produce a force in toward the centre of the curve. Now it is obvious that the road does not know when we wish to turn so it must be the tyre, through the signals that the rider feeds to it, that starts the process. The detail mechanisms of how this actually happens is less obvious and more involved than may appear at first sight. Those who drive as well as ride may have wondered why it is necessary to turn the front wheels more on a car, than on a bike, to take the same corner at the same speed. The essential difference is that a bike must lean inwards when cornering to maintain balance, whereas a car remains substantially upright. Consider a wheel, held upright as on a car, following a curved path as in fig.1., if this wheel is aligned with the direction of the curve at any particular point on it (i.e. pointing in the direction of travel) then the wheel will tend to go straight on along a tangent to the curve and will generate no cornering force.

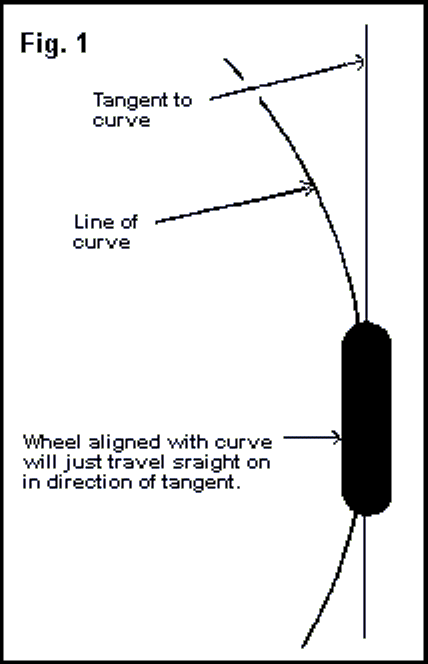
Clearly then, something else must be done in order to persuade the tyre/road junction to generate the centrifugal/centripedal force required. On a car or other self balancing vehicle this is done by turning the wheel in more than the line of the curve. The angle between the direction of the tyre and the tangent to the curve is known as the 'slip angle'. Reference to fig.2. will help explain how this works.

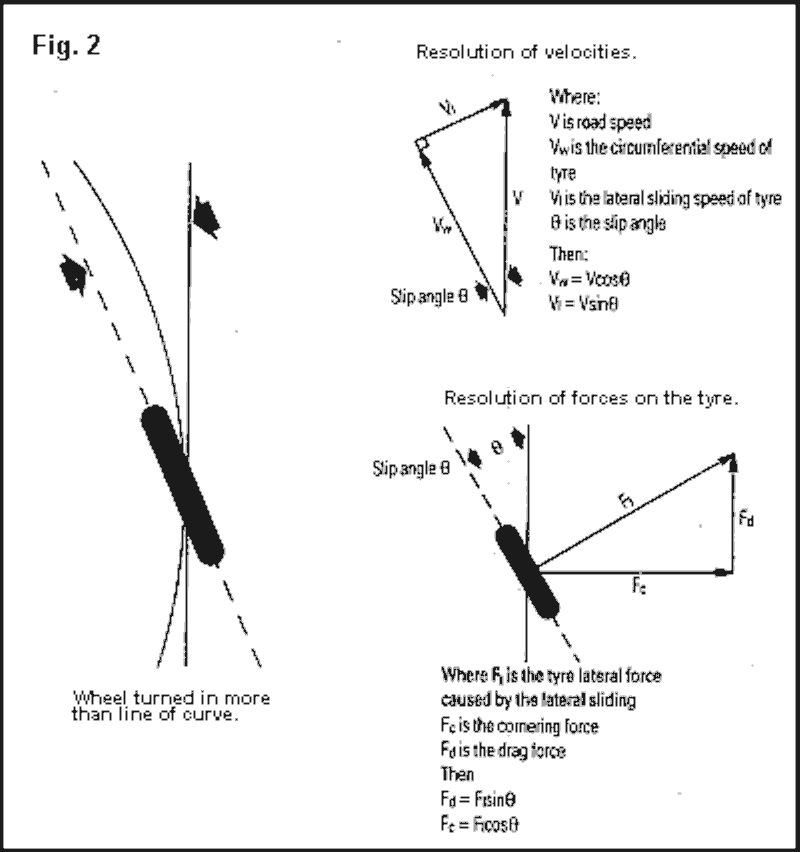
As the wheel is now no longer travelling exactly in the direction in which it is pointing, we can resolve its velocity tangent to the curve into components aligned with the wheel and at right angles to it. This means that the peripheral tyre speed will be slightly less than the road speed around the turn but there is now a sideways speed to the tyre, i.e. is it is sliding sideways. This lateral movement produces a force at right angles to the wheel direction. The magnitude of this force depends on the amount of slip angle, increasing up to about 15° and then falling off rapidly, that's when the driver has lost it. This wheel lateral force can now be resolved into a component at right angles to the direction of travel, cornering force, and into one aligned with the direction of travel, a drag force. It is this drag force which causes a car to slow when driven hard around a bend under constant power. So, we can now see what generates and controls the forces that cause a car to corner, and why the wheels must turn more than the amount just necessary to align with the direction of the curve. Fig.3. shows the rear view of a lent over bike wheel and how it can be considered as a cut off section of a cone.

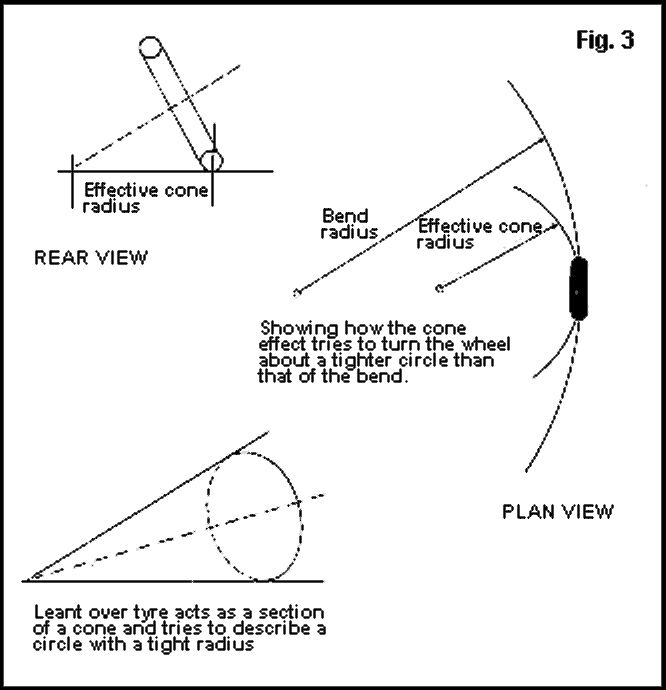
As the inside edge of the tyre is forced to adopt a smaller radius than the outer edge, then for a given wheel rotational speed, the inner edge would prefer to travel at a smaller road speed, this happens if the wheel is allowed to turn about a vertical axis through the point of the cone. Just as a solid cone on a table if given a push. But if the bike was leaning over at 45° then for a normal size tyre the horizontal radius to the cone axis would be approximately 1.5 feet, an impossibly tight turn. However, attempting this turn will generate a centrifugal force which tends to throw the bike away from the centre of the turn and hence it will describe a larger radius. This then is the main mechanism for generating the cornering force on a bike, and is often referred to and misunderstood as "CAMBER THRUST". To reiterate, As the wheel leans over, --- cambers ---, it tries to behave as part of a cone and turn a very tight corner, but the centrifugal force then generated forces this tight curve to straighten out and follow the turn radius that the rider desires.

Thus cornering force can be generated without the slip angle so necessary on a car.

But, because the camber angle of the bike is determined by the need to balance the machine for a given speed around a given corner, it is unlikely that in all cases will the camber thrust be of exactly the correct amount. e.g. Tyre size and compound will affect this force for a particular angle of lean. Therefore, it is necessary to have an additional method to correct the cornering force to that which we need to negotiate the turn in question. This is simply done by introducing a small slip angle by means of the handlebars. If the camber thrust generated is insufficient to match the cornering force needed, then we just turn the bars a bit more into the corner, or in other words introduce a positive slip angle. Under those circumstances where excess cornering force is available it becomes necessary to apply negative slip angles, i.e. to steer out of the turn. So next time that you see a picture of some race ace with the front wheel set up with a small amount of opposite lock, do not immediately assume that the rider is drifting wildly. His wide grippy tyres may just simply produce too much camber thrust which needs detuning with a negative slip angle. The 'position' of the handlebars depends on the required slip angle, but the 'torque' to be applied to achieve this position depends on many other factors. Wheel diameter, tyre width, rake and trail are but some of the influencing parameters. On some machines it may even be essential to apply a negative torque to maintain a positive slip angle at the required level, the geometry may try and force the bike on to a tighter line if left to its own devices. A bike set up like this, tends to flop over easily, and may give the feeling that the rider needs to hold it up. Whereas another type of machine may need a positive torque to maintain the desired steering angle and this bike will feel as if it needs to be held down. A few numbers may help to show how different speeds and bend radii affect the lean angle and hence the effective cone radius, and camber thrust. -- When cornering at an angle of 45° and 70mph. the turn radius will be 327 ft. and at half that speed, 35mph., the radius will be a quarter of that or 82 ft. --- but as shown earlier the cone radius will be only 1.5 ft.

We can see that there is a very large difference between the bend radius and the effective cone radius, the tight cone radius generates a lot of camber thrust to support the large cornering forces present at a 45° lean angle. Now, if we slow down to 7mph. and tackle the same corners, we would need to lean over to only 2.5° and the cone radius would be up to 25 ft., for the 82 ft. radius bend, 0.57° camber angle and a cone radius of 100 ft. would be appropriate for the 327 ft. bend. For these cases the cone radii are much larger and are up to approximately 1/3 of the bend radii. Consequently the camber thrust is much reduced, in line with the smaller requirement of these gentle cornering speeds.

Those of you that have followed racing techniques over the past few years will be aware of a change in riding styles amongst the really fast riders, who now drift their machines to quite a significant extent. Fig. 4. shows an extreme case of drifting, as would be experienced in speedway.

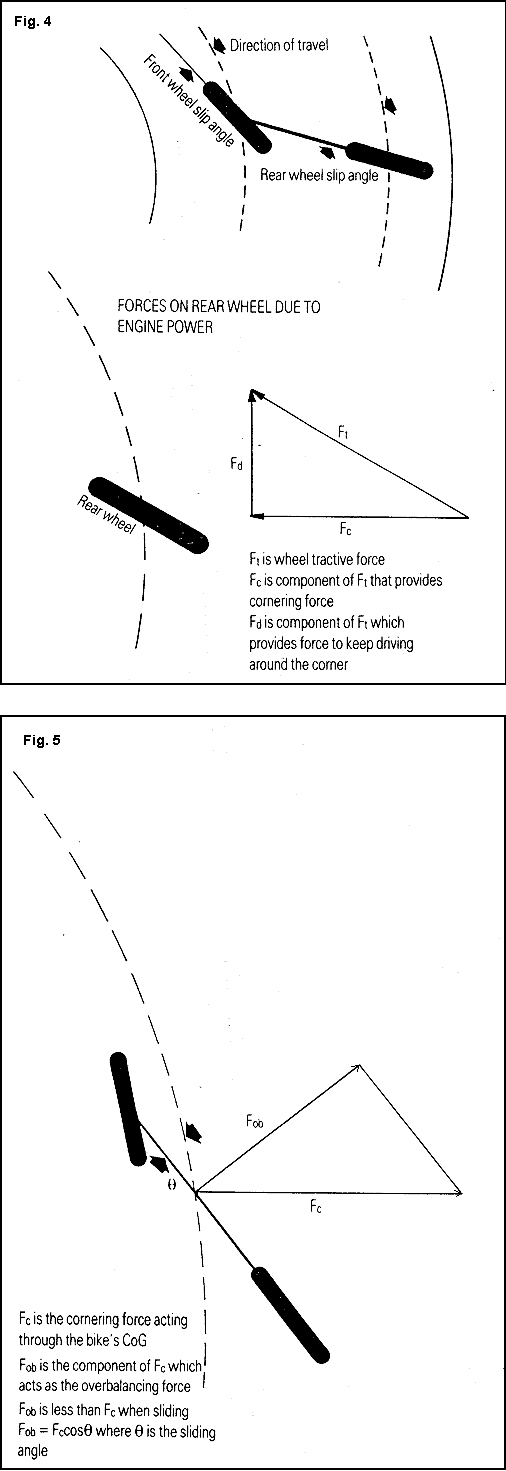
The cornering force is provided from two sources:

1. Camber thrust and slip angle as described above.

2. The component of the engine supplied driving force, that acts toward the centre of the corner. This driving force itself, acts in line with the rear wheel, but as this is at a significant angle to the direction of travel it can be resolved into two components. One of which acts in the direction of travel and maintains the speed around the curve, the other acts at right angles to this, and pushes the bike toward the centre of the curve, i.e. provides some cornering force. Because the front wheel is not driven it must produce its share of the cornering force by more normal means. But, as this wheel is more upright than in the non sliding case, camber thrust is reduced and so more of the cornering force must come from a slip angle, and the wheel will be turned more into the corner, than if the rear wheel was sliding less. As a large part of the total cornering effort is derieved from the engine power, it comes as no surprise that throttle position has a major influence over the cornering line. It has been demonstrated countless times in speedway that mid-corner engine failure or inexperienced shutting of the throttle, results in immediate intimate inspection of the perimeter fencing. This sudden loss of engine power results in an equally sudden loss of cornering power, and the bike succumbs to the effects of centrifugal force. The required lean angle varies as the angle of sliding changes (rear wheel slip angle), the reason for this can be seen in fig.5. the over-balancing force acting on the bike is the component of the cornering force that acts at right angles to the line of the machine.

So the greater is the sliding angle, the smaller is the over-balancing tendency that needs compensating by leaning in. Thus, a smaller angle of lean is needed, but the effect of this is often over stated, as a few more figures will demonstrate. Imagine a road racer cornering at 1G. lateral acceleration, and let's assume that the rear wheel is 1 ft. out of line with the front, and that the wheelbase is 57", then the sliding angle is 12° . Without sliding at all the lean angle of the combined bike and rider would be 45° , but when sliding at 12° this camber angle reduces to 44.4° , hardly a big difference! To return to speedway cornering styles, where a more typical slide angle may be, say, 50° , then again for the 1G. case the lean angle reduces to 33° . So we can see that to reduce the lean angle by a significant amount requires a high degree of drifting, more in fact than is usual in road racing. So where is the benefit in sliding? --- Well, as any drag racer knows maximum traction is achieved when the tyre is spinning slightly. In fact the tyre companies tell us that approximately 10-20% slip is about optimum on tarmac. So if sufficient power is available to cause this degree of spin the total friction force on the tyre is increased slightly and some of this can be resolved towards the bend centre,( if the bike is in a drifting attitude ), thus increasing cornering force and speed.

The extreme drifting in speedway is necessary for slightly different reasons. The loose surface is incapable of supporting high cornering forces through the normal mechanisms of camber thrust and slip angle, but considerable force can be generated by a spinning rear wheel. Some of this is just due to the usual frictional processes, but an added effect comes from the rooster tail of shale thrown up behind. The tyre has to put effort into imparting momentum to these rocky particles and so in accordence with the previously mentioned law of Newton, these particles must push back onto the tyre. This is similar to the principle of a rocket, where the rapid ejection of combustion material pushes it along. To take advantage of this rocket powered effect in a bend, requires the bike to be pointing toward the turn centre so that a significant component of this force is used as cornering effort.

SUMMARY

A car derieves its cornering force by means of a slip angle, which is to say that the driver turns the wheels in more than the line of the bend. As if he wanted to take a tighter curve. A bike on the other-hand achieves the same end through an effect known as camber thrust, which is a consequence of leaning into a corner. The tyre then acts like part of a cone and tries to turn a tighter circle than the actual bend. Centrifugal force straightens this circle closer to the desired path, and relatively small slip angles are then used to correct any errors. The foregoing applies at normal speeds upwards, at very slow speeds the lean angle is small and the steering angles are greater.

There is some similarity between the mechanisms of steering both bikes and cars. i.e. it is necessary in both cases to set up a tendency for each vehicle to try and turn around a tighter bend than the radius desired. It is just the method of generating this tendency that differs. Drifting is a useful way of using excess engine power to provide some additional cornering power, but on tarmac the reduction in lean angle is not usually all that much. The increased racing use of this technique has been made possible by the vast power outputs of modern engines.

Isn't physics fun?